数学が苦手なハッカーでもわかる、RSA暗号の基本を学ぶ

実は、私は「数式アレルギー」なのです。見ただけでやる気が失せます。
だから、私が理解できるレベルまで落として説明しますね。(^^)
目次
RSAとは
「暗号」と聞くと難しそうに思えるかもしれません。
たとえば、インターネットでメッセージを送るとき、当然ほかの人に見られたくないですよね。たとえば、LINEのメッセージやパスワード、クレジットカードの番号などです。

そんなときに役立つのが「暗号」です。その中でもよく使われているのが「RSA(アールエスエー)」という暗号のしくみです。
CTF(Capture The Flag)でも、このRSAを使った問題がたくさん出ます。
まずは、数学が苦手な人でも安心して読めるように、RSAの基本をやさしく紹介していきます。
RSA暗号を簡単に説明します
RSA暗号は、次の2つの鍵を使います。
・公開鍵:だれでも使っていい。メッセージにカギをかける道具。
・秘密鍵:自分だけが知っている。カギを開けるための道具。
たとえば、ロッカーでたとえると
・ロッカーの番号が「n」
・カギの種類が「e」
・カギを開ける道具が「d」
という風になります。

誰でもロッカーに手紙(メッセージ)を入れることはできるけど、開けられるのは本物のカギを持ってる人だけ、というイメージです。
RSAの基本式をざっくり理解
RSAでは次のような計算を使って暗号を作ったり、元に戻したりします。
メッセージ m を暗号文 c に変える式は。
c = m^e mod n
つまり、「メッセージのe乗をnで割ったあまり」が暗号です。
復号(元に戻す)は、c^d mod n という式でできます。
わかりましたか?
c = m^e mod n
c^d mod n
私には、チンプンカンプンです。熱が出てきました。(^^;

RSAの作成方法の優しく説明
極力わかりやすく説明します。
1.変数の説明
記号 意味
m:メッセージ(手紙)
c:暗号文(暗号に変わった手紙)
n:大きな数(暗号ロッカーの番号)
e:公開カギ(みんなに公開していい「暗号ロッカーに手紙をいれるカギ」)
d:秘密カギ(こっそり持ってる「暗号ロッカーから手紙をとりだすためのカギ」)
※MOD関数とは、数値を除数で割ったときの余りを求める関数です。例えば、MOD(10, 3)は1を返します。これは、10を3で割ったときの余りが1だからです。
2.まず、2つの素数を決めます。(pとq)
たとえば、
p = 5
q = 11
とします。(素数ならなんでも良いです。)
3.大きな数(暗号ロッカーの番号)のnを求めます。
計算式は、n = p × q
よってnは、5 × 11 = 55

※"n" の大きな数(暗号ロッカーの番号)は55
4.秘密鍵を計算するのに必要なφ(n) を求めます。
φ(n)は「秘密鍵を計算するのに必要な特別な数」です。
式は、φ(n) = ( p-1 )( q-1 )
よってφ(n)は ( 5-1 )( 11-1 )
4 × 10 = 40 となります。
5.eの公開カギを求めます。
e は φ(n) と「互いに素」(=共通の約数が1)である小さい数を選びます。
・・・と言われても、私は全然分かりません。
「互いに素」とは。
2つ以上の整数について、それらの最大公約数が1である状態を指します。
つまり、1以外に共通の約数を持たないことを意味します。
例えば、3と5は互いに素です。
上記の例であれば、
| φ(n) | 公開カギ | 共通の約数 互いに素か | ||
| 40 | 3 | はい | ||
| 40 | 4 | いいえ | ||
| 40 | 7 | はい | ||
| 40 | 10 | いいえ | ||
| … | … | … | ||
| 40 | 65537 | はい | ||
| … | … | … | : | : |
となり、3,7,...65537などは共通の約数が1のため、eの公開カギの対象になります。
上記のように対象の公開鍵が複数あります。
ここで、φ(n) = 40 と「互いに素」な数の中から、1つ選びます。
e = 3(すごく小さくて計算が早い)
e = 65537(安全で使いやすいが、計算に時間がかかる)
などがありますが、
今回はわかりやすくて小さい数の「e = 3」にしました。
3と40は「互いに素」だから条件OKですね。
小さな数だから、暗号化の計算も楽になります。

※"e"の公開カギは3
6.dの秘密鍵を求める
計算式は、d × e ≡ 1 modφ(n)
つまり
d × 3 ≡ 1 mod40
この式を満たす d を見つけるには、次のように探します。
| d | d×3 | d×3 mod 40 |
| 1 | 3 | 3 |
| 2 | 6 | 6 |
| … | … | … |
| 27 | 81 | 1(余りが1) |
d × 3 mod 40が1であるため、秘密鍵 d = 27になります。
(d = 27 は、「3 × 27 を 40で割ると 1 になるから」です。)

※"d"の秘密鍵は27
結論
n:大きな数 55
e:公開カギ 3
d:秘密カギ 27
となりました。
RSAで作成した「大きな数」「公開カギ」「秘密カギ」の検証
メッセージを「3」に、大きな数(n)を「55」、公開カギ(e)を「3」で暗号にします。
メッセージを「3」にしているのは計算時間を短くするためです。
そして、秘密カギ(d)を「27」で復号します。(元に戻します)
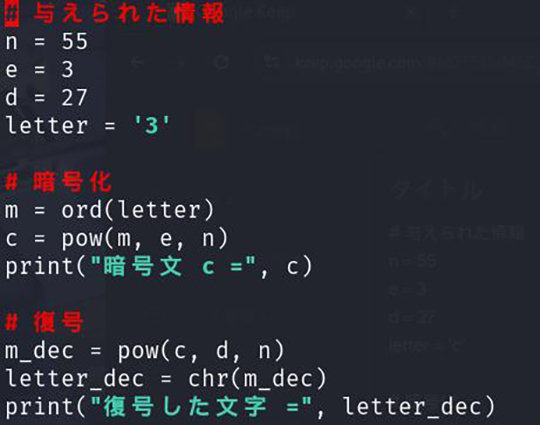
【pythonコード】
# 与えられた情報
n = 55
e = 3
d = 27
msg = '3'
# 暗号化
m = ord(msg)
c = pow(m, e, n)
print("暗号文 c =", c)
# 復号
m_dec = pow(c, d, n)
msg_dec = chr(m_dec)
print("復号した文字 =", msg_dec)
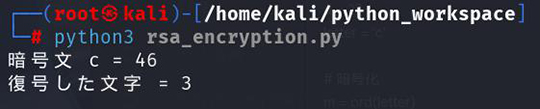
計算結果は以下のとおりです。
暗号文 c = 46
復号した文字 = 3
メッセージ"3"を暗号化すると"46"
"46"を復号すると"3"になりました。
今回は、メッセージが"3"でしたが、メッセージを長くするためには、上部の2つの素数(pとq)を大きくする必要があります。
CTFで出てくるRSA問題のためには
CTFでは、RSAの弱点をついた問題が出ます。
でもいきなり攻撃方法を学ぶのではなく、まずは以下の基本を押さえるのが大切です。
公開鍵と秘密鍵の関係
「暗号化に秘密鍵は使わない」理由(→ 公開鍵だけでカギをかけられるから)
この基本がわかっていれば、今後出てくる "こわれたRSA" のパターンにも対応しやすくなります。
数学が苦手なハッカーでもわかる、RSA暗号の基本を学ぶのまとめ
RSA暗号は、一見むずかしそうに見えるかもしれません。でも、実は「ロッカーとカギ」のたとえで考えると、とてもイメージしやすいものです。
CTFでは、RSAを完全に理解する必要はありません。
・なにが起きているのかをイメージする
・よく出るパターンを覚える
・難しい計算はPythonなどのツールにまかせる
これで、あなたもCTFのRSAの入口に立つことができましたね。













